푼 날짜 : 2024.11.16
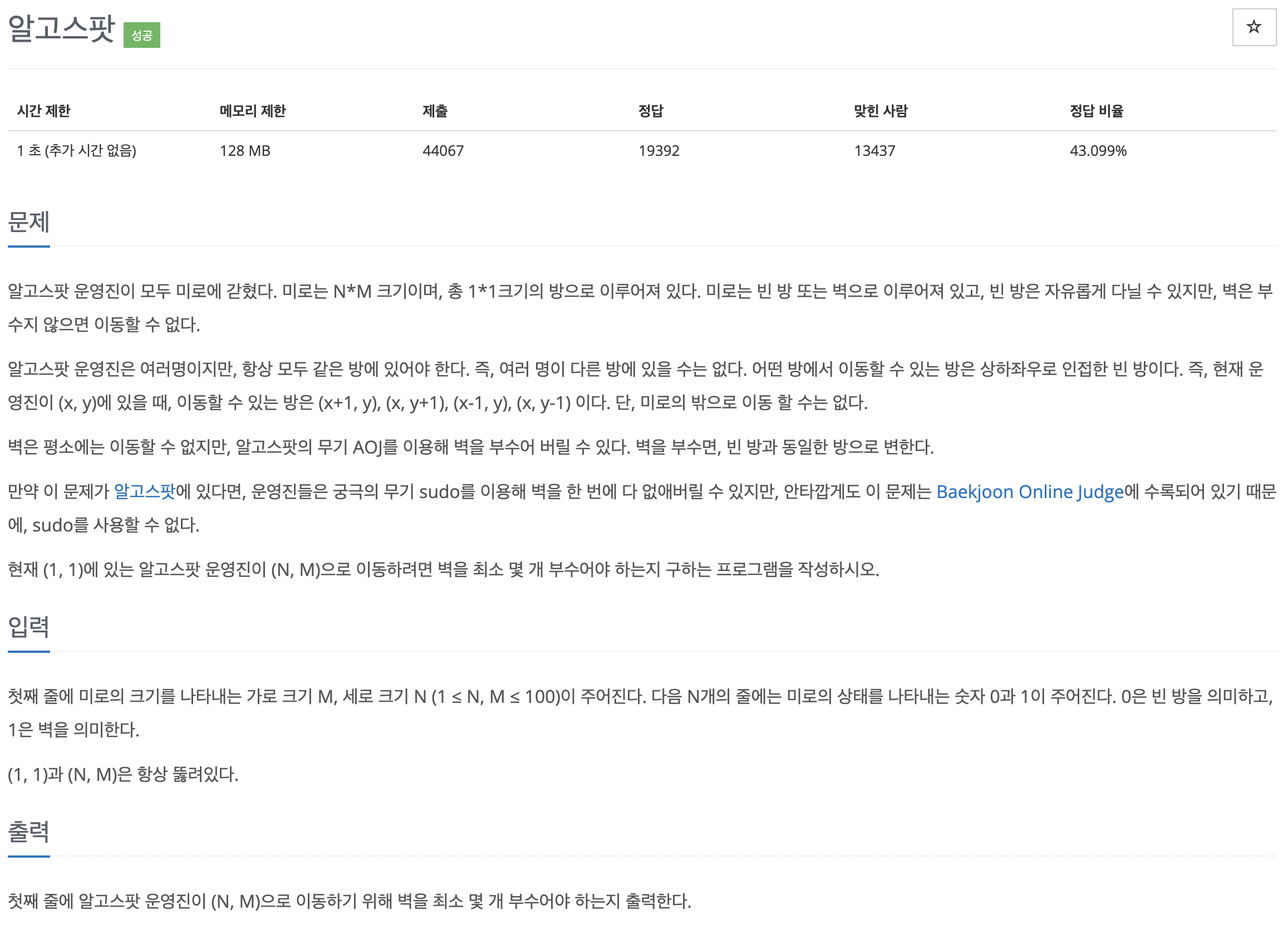
푼 문제 : [1261] / 알고스팟
사용한 언어 : python
알고리즘 : 다익스트라(dijkstra)
접근방식 :
현재위치가 x, y 일때 (x+1, y), (x, y+1), (x-1, y), (x, y-1) 모두 탐색 가능하므로 4방향 탐색을 진행한다.
이때 값이 더 작은 경우 업데이트 해주고 아니라면 넘어간다.
최종 목적지까지 반복하면 벽을 최소한으로 부순 값을 알 수 있다.
코드 :
import sys
import heapq
N, M = map(int, sys.stdin.readline().split())
graph = []
for _ in range(M):
lst = list(sys.stdin.readline().rstrip())
graph.append(lst)
visited = [[float("INF") for _ in range(N)] for _ in range(M)]
visited[0][0] = 0
dy = [-1, 1, 0, 0]
dx = [0, 0, -1, 1]
# cost, i, j
heap = [(0, 0, 0)]
while heap:
now_cost, now_i, now_j = heapq.heappop(heap)
# 상하좌우 계산
for j in range(4):
ny, nx = now_i + dy[j], now_j + dx[j]
# 적절한 범위의 값일 때
if 0<=ny<M and 0<=nx<N:
all_cost = now_cost + int(graph[ny][nx])
# 비용이 더 작을 때
if visited[ny][nx] > all_cost:
visited[ny][nx] = all_cost
heapq.heappush(heap, (all_cost, ny, nx))
# 최종적으로 도착지에서 뿌신 벽의 수
print(visited[M-1][N-1])
탐색이랑 응용되니 더 재밌는 문제~!
'Programming > Algorithm' 카테고리의 다른 글
| [백준4485] / 녹색 옷 입은 애가 젤다지? - 다익스트라/그래프탐색 (1) | 2024.11.19 |
|---|---|
| [백준17396] / 백도어 - 다익스트라 (0) | 2024.11.17 |
| [백준23793] / 두 단계 최단 경로 1 - 다익스트라 (2) | 2024.11.15 |
| [백준18223] / 민준이와 마산 그리고 건우 - 다익스트라 (2) | 2024.11.15 |
| [백준2211] / 네트워크 복구 - 다익스트라 (0) | 2024.11.14 |
